关键路径法简介

2024-07-14

关键路径法简介

一个大型工程或项目包括很多活动，关键路径是项目中时间最长的活动顺序，决定着可能的项目最短工期。

关键路径法（Critical path method，CPM） 是一种基于进度网络模型的方法，用网络图表示各项活动之间的相互关系，获得在一定工期、成本、资源约束条件下的最优进度安排。

关键路径法源于美国杜邦公司对于项目管理控制成本、减少工期的研究。1959年，Kelly 和 Walker 在论文 Critical Path Planning and Scheduling 中提出了关键路径法的基本原理和方法：计算所有活动的工期，确定其最早开始 ES 和最早结束 EF、最晚开始 LS 和最晚结束 LF 的时间，按照活动的相互关系形成顺序的网络逻辑 图，找到必须的最长路径即为关键路径。

关键路径法将项目分解成为多个独立的活动并确定每个活动的工期，然后用逻辑关系（结束-开始、结束-结束、开始-开始和开始-结束）将活动连接。首先使用正推法（Forward pass），从起点开始向后计算，依次计算每个顶点（事件）的最早开始时间 ES；然后再使用逆推法（Backward pass），从终点开始向前计算，依次计算每个顶点（事件）的最迟结束时间 LF。进而可以求出每条边（工序）的最早结束时间 EF 和最迟开始时间 LS。最早开始时间 ES 和最晚开始时间 LS 相等的边，就是关键路径上的边，对应的工序是关键工序。

  • ES：最早开始时间（Earliest Start），指某项活动能够开始的最早时间，取决于该项活动的所有紧前工作的结束时间，由顺推法计算 ES = max{EF(preceding activities)}。
  • EF：最早结束时间（Earliest Finish），指某项活动能够完成的最早时间。EF = ES+DU， DU为该活动的持续时间。
  • LF：最迟结束时间（Latest Finish），指为了保证整个项目按期完成的某项活动必须完成的最晚时间，取决于该项活动的所有紧后工作的最迟开始时间，由逆推法计算 LF = min{LS(successor activities)}。
  • LS：最迟开始时间（Latest Start），指为了保证整个项目按期完成的某项活动必须开始的最迟时间。LS = LF -DU，DU为该活动的持续时间。
  • TF：总时差（Total float time），指在不影响总工期的条件下，一个活动可以利用的机动时间。TF = LF - EF。
  • FF：自由时差（Free float time），指在不影响紧后工作最早开始时间的条件下，一个活动可能被延迟的时间。FF = min{ES(successor activities)} - EF。
    由关键路径法得到的最早/最晚的开始/结束时间并不一定就是项目进度计划，而是把既定的参数（活动持续时间、逻辑关系、提前量、滞后量和其它制约条件）输入进度模型后所得到的结果，表明活动可以在该时段内实施。

早期关键路径法的表示方法都是箭线法（ADM），随着计算机的发展，前导图（PDM）逐渐成为主流方法。

关键路径法

某项目工程由 11项作业组成（分别用 A、B、…K表示），其计划完成时间及作业间相互关系如下表所示。建立计划网络图，并计算完成该项目的最短时间。

作业 计划完成天数 紧前工序 作业 计划完成天数 紧前工序
A 5 无 G 21 B,E
B 10 无 H 35 B,E
C 11 无 I 25 B,E
D 4 B J 15 F,G,I
E 4 A K 20 F,G
F 15 C,D . . .
本案例问题来自：司守奎、孙兆亮，数学建模算法与应用（第2版），P62-68，例4.16-4.18，国防工业出版社。

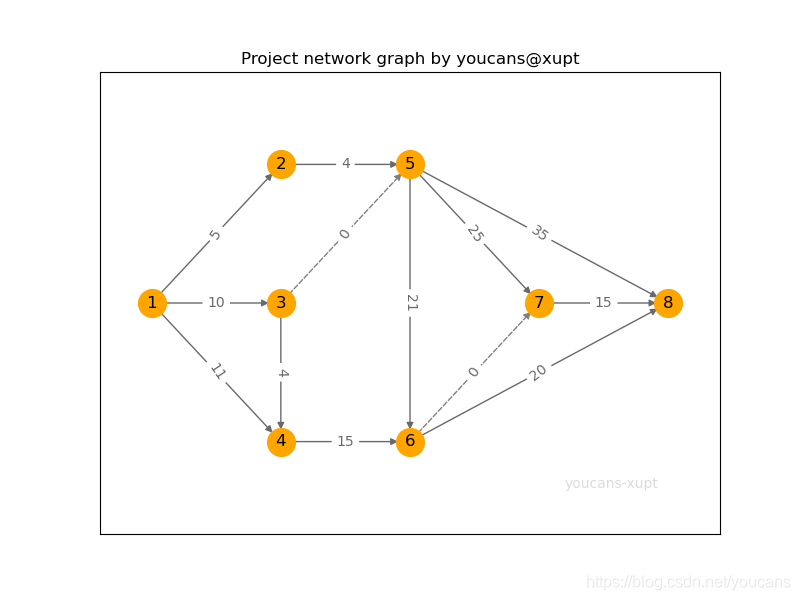
问题分析： 用如下图所示的计划网络图表示问题描述的各项作业及作业间的相互关系。图中的顶点表示作业开始或结束的事件，顶点之间的边（箭线）表示一项作业，边的权值表示该项作业的完成时间。虚线边表示虚拟作业。 该计划网络图的关键路径长度，即为完成该项目的最短时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# mathmodel23_v1.py
# Demo23 of mathematical modeling algorithm
# Demo of critical path method (CPM)  with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated：2021-07-25

import numpy as np
import matplotlib.pyplot as plt  # 导入 Matplotlib 工具包
import networkx as nx  # 导入 NetworkX 工具包

# 1. 拓扑序列(topological sequence) 和 关键路径(critical path)
# Activity on edge network(AOE), 顶点表示事件或状态，有向边表示活动
DG = nx.DiGraph()  # 创建：空的 有向图
DG.add_weighted_edges_from([(1, 2, 5), (1, 3, 10), (1, 4, 11),
                            (2, 5, 4),
                            (3, 4, 4), (3, 5, 0),
                            (4, 6, 15),
                            (5, 6, 21), (5, 7, 25), (5, 8, 35),
                            (6, 7, 0), (6, 8, 20),
                            (7, 8, 15)])  # 向图中添加多条赋权边: (n1,n2,weight)
lenNodes = len(DG.nodes)  # 顶点数量
topoSeq = list(nx.topological_sort(DG))  # 拓扑序列
nodeCP = list(nx.dag_longest_path(DG))  # 关键路径（节点）
lenCP = nx.dag_longest_path_length(DG)  # 关键路径的长度
edgesCP=[]
for k in range(1,len(nodeCP)):
    edgesCP.append((nodeCP[k-1],nodeCP[k]))

print("拓扑序列：{}".format(topoSeq))  # [1, 3, 4, 2, 5, 6, 7, 8]
print("关键路径的顶点：{}".format(nodeCP))  # [1, 3, 5, 6, 8]
print("关键路径的边：{}".format(edgesCP))  # [(1, 3), (3, 5), (5, 6), (6, 8)]
print("关键路径长度：{}".format(lenCP))  # 51

fig, ax = plt.subplots(figsize=(8,6))
pos = {1:(0,4), 2:(5,7), 3:(5,4), 4:(5,1), 5:(10,7), 6:(10,1), 7:(15,4), 8:(20,4)}  # 指定顶点位置
edgesDG = DG.edges
edgesDashed = [(3,5),(6,7)]
edgesSolid = list(set(edgesDG)-set(edgesDashed))
labels = nx.get_edge_attributes(DG, 'weight')
# nx.draw(DG, pos, with_labels=True, node_color='skyblue')  # 绘制有向图
nx.draw_networkx_nodes(DG, pos, node_color='orange',node_size=400)  # 设置指定顶点的颜色、宽度
nx.draw_networkx_labels(DG, pos)  # 设置指定顶点的标签
nx.draw_networkx_edges(DG, pos, edgelist=edgesSolid, edge_color='dimgrey', style='solid')  # 设置指定边的颜色、线型
nx.draw_networkx_edges(DG, pos, edgelist=edgesDashed, edge_color='grey', style='dashed')  # 设置指定边，虚线
nx.draw_networkx_edge_labels(DG, pos, edge_labels=labels, font_color='dimgrey')  # 显示边的权值
ax.set_title("Project network graph by youcans@xupt")
ax.text(16, 0, "youcans-xupt", color='gainsboro')
plt.xlim(-2, 22)
plt.ylim(-1, 9)
plt.axis('on')
plt.show()  # YouCans, XUPT

程序运行结果：

拓扑序列：[1, 3, 4, 2, 5, 6, 7, 8]
关键路径的顶点：[1, 3, 5, 6, 8]
关键路径的边：[(1, 3), (3, 5), (5, 6), (6, 8)]
关键路径长度：51

原文链接：(https://blog.csdn.net/youcans/article/details/118754623)